A Grand Unified Theory with the Axial Force
Understanding this section, requires a good knowledge of the standard model of particle physics, if your understanding of the SM is limited,try reading my description of the standard model here.
Does our axial force help build a grand unified theory? We think so, because keeping both the axial and electric charges conserved automatically keeps
the proton stable. We however find that we need to double the number of quarks, this may seem a step backwards (but see later). Why double the
number of quarks? Well our axial force has opposite charge on the left and right handed particles, which means the have either transform to something
else when you overtake them, or keep the same spin. But Protons and Neutrons seem to reflect they spins just fine. Then in order to let the quarks keep
the same charge under reflection, we need a another pair of heavier quarks per generation that they can transform to thus we get.


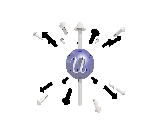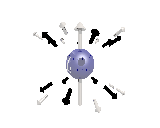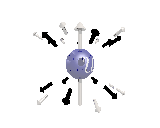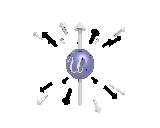
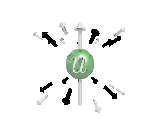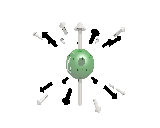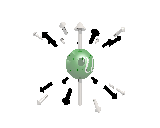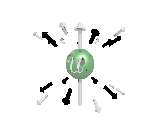
Where the black arrows represent the electric field and the grey arrows the axial field. By mixing the particles we arrive at mass states with the
same axial charge on both the right and left handed particles. Adding these heavy tera-quark states, turns the 15 particles for one generation of
the standard model, in a group of 27 particles. One 27 particle group, is the fundamental representations of the exceptional group E6. Let arrange
the particles as below. [Warning wide browser required]







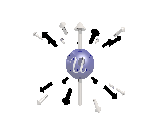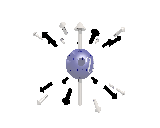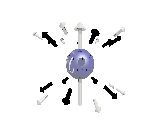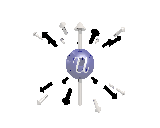
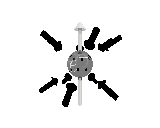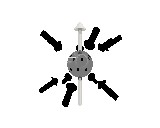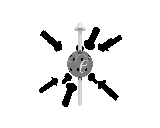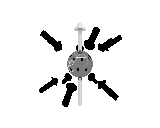
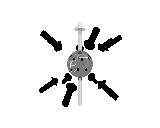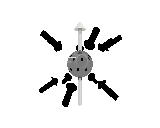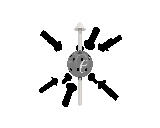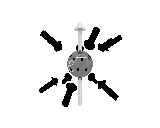


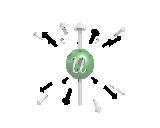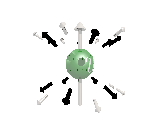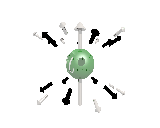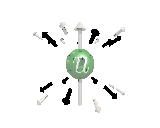


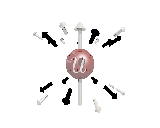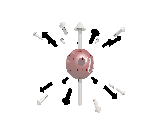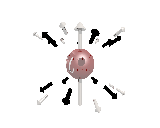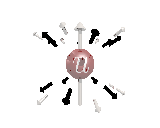

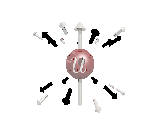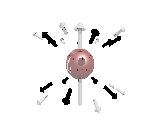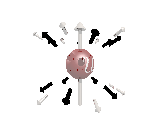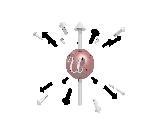


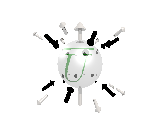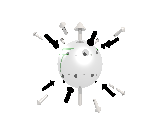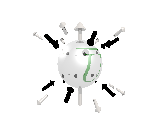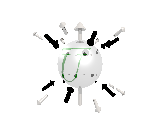




The above makes up a 27 particle representation of the group E6. E6 is know to be a chiral group, that is it can break left-right symmetry,
in the above only a left handed weak force should be present. Two copies of E6 and two the right handed neutrinos, make up the non
chiral group E7.
E7 ~ E6 + (anti E6) + (1) + (anti 1).
But even better three generations of E6's and the antiparticles fit exactly into String theorys favourite group E8.
E8 ~ (8) + (78, E6 adjoint) + 3*(E6) + 3*(anti E6).
The E6 adjoint gives (under supersymmetry) the forces acting universally on each generation.
The right handed neutrinos needed for the axial force, are missing and presummably fall into the remaining 8 particles, which permute the
generation number, as below.
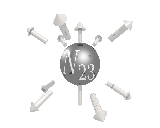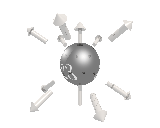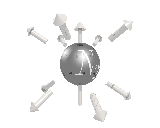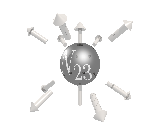


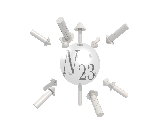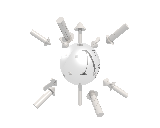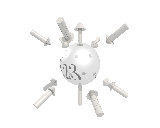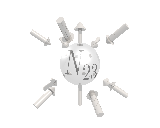

So we've explained the left/right symmetry breaking, and the 3 generations of quarks and leptons, with this model. We also predict one extra
right handed neutrino, that doesn't feel the axial force. And we seem to predict tri-bimaxially neutrino mixing. However there is no room for
Higgs bosons in it. The Higgs will have to be composite particles builts from interactions between some of the above fermions. Some chiral
condensate needs to form to give the particles mass. It should be noted that all this is speculation not yet backed up by any concrete math.